方法

首先，根据从重叠图像重新投影的 3D 点计算两个模型之间的全局相似性变换矩阵。

之后，重叠图像的相机参数和一个模型中的重新投影的 3D 点使用获得的全局相似性变换矩阵进行细化。

最后，根据内部 2D-3D 对应估计两个 3D 模型之间的精确相似性变换矩阵，以准确对齐和合并两个 3D 模型。

对比

常见的稀疏 3D 模型合并方法将相似变换矩阵估计技术之一与 RANSAC 相结合。

然而，一个重要的问题是，如果模型对齐偏向重叠区域中的某些部分，则合并后的模型可能会出现全局对齐错误。

改进

所提出的方法首先计算全局相似变换矩阵以减少全局未对齐问题。使用获得的全局相似性变换矩阵，所提出的方法细化了子模型的重叠区域。由于重叠区域的细化过程，可以更准确地对齐两个子模型。所提出的方法计算精确的相似变换矩阵并合并两个子模型。

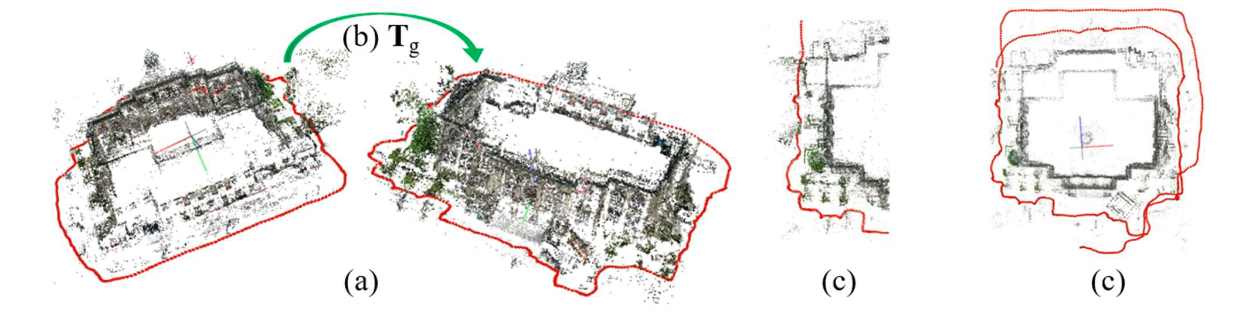
给定两个具有重叠图像和2D-3D对应关系的子模型，提出的方法

• （a）计算子模型1和2的重新投入误差的平均值，
• （b）计算重叠区域之间的全局相似性转换矩阵
• （C ）使用全局相似性变换矩阵来完善子模型M1中的重叠区域，并且
• （d）计算重叠区域之间的精确相似性转换矩阵，并合并两个子模型。

给定两个稀疏3D模型M1,M2，具有重叠区域(R)M1，(R)M2，由已知的 2D-3D 对应关系和相机参数 {$P_i$}M1 和 { $P_i$}M2 的共享图像 {$I_i$}，所提出的方法执行以下过程

Step1. 计算每个子模型的重叠区域的重投影误差的平均值，假设(R)M2的重投影误差均值低于(R)M1的

Step2. 使用RANSAC筛选3D点来计算全局相似变换$T_g$，所选择3D内点$X_j$满足以下约束

$$\text{ i) }\frac{1}{T_j}\{{({\mathbf{x}}_j^i-{\mathbf{P}}_i{\mathbf{T}}_{\mathrm{g}}^{-1}{\left({\mathbf{X}}_j\right)}_{\mathrm{M}2})}_{\mathrm{M}1}^2+{({\mathbf{x}}_j^i-{\mathbf{P}}_i{\mathbf{T}}_{\mathrm{g}}{\left({\mathbf{X}}_j\right)}_{\mathrm{M}1})}_{\mathrm{M}2}^2\}\le r_{\text{thres }}$$$$\text{ii) }{T}_j\ge T_{thres}$$

其中$T_j$为$X_j$对应的track 长度，本文设置rthres=6, Tthres = 5。有了3D内点，应用方法[7]计算从M1到M2的全局相似变换$T_g$。

Step3. 将M1中的$I_i$的相机参数${P_i}_{M1}$替换为${P_i{T}_g}_{M2}$ ，然后将具有2D-3D对应关系的相机参数${P_i{T}_g}_{M2}$ 的局部BA应用到M1。

Step4. 选择内点2D-3D对应关系获得精确的相似变换矩阵$T_m$，内点$(x_j^i,X_j)$ 满足上述的$i,ii$，以及下面的条件

$$\underset{i}{min}\{{({\mathbf{x}}_j^i-{\mathbf{P}}_i{\mathbf{X}}_j)}_{\mathrm{M}1}^2+{({\mathbf{x}}_j^i-{\mathbf{P}}_i{\mathbf{X}}_j)}_{\mathrm{M}2}^2\}$$

在选择完内点后，应用[5]来计算从M1到M2的精确相似变换矩阵$T_m$，来执行两个子模型M1和M2的合并过程。